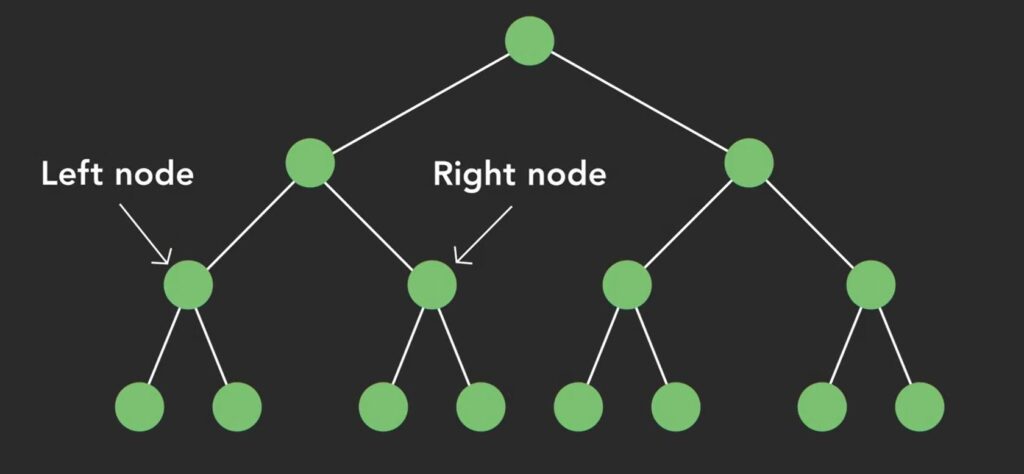
A binary tree is a specialized type of tree. It adds the constraint that each node has two immediate child nodes. More terminology here. We call the child nodes left and right nodes respectively. The left child node and the right child node could both be null, both have values, or one of them could be null. What happens with a binary search tree, also called a BST? A binary search tree is also a specialized type where we add an additional constraint, order. In a BST, we keep track of order and keep a sorted data structure by being particular about what values are in the left child, right child, and parent nodes. Why do this? It makes the data structure more than just a collection of stuff strung together. It’s a data structure that naturally stays sorted without immense amounts of reshuffling that would be needed in a basic array. What’s the rule? A left child node must be less than its parent and a right child node must be more than its parent. That rule follows all the way down. As we insert new nodes with values, the tree must always stay sorted. A binary search tree is often used to sort key value pairs. What we’d be representing here is the key to an object.