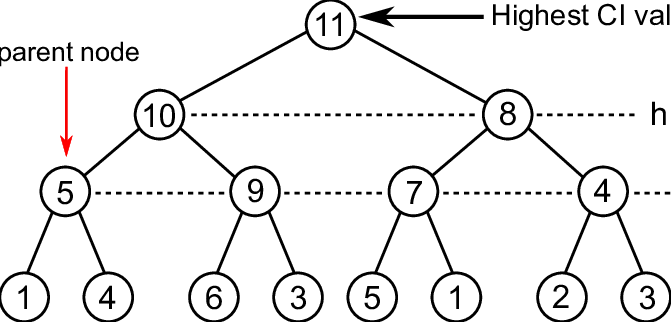
A heap is a data structure that’s implemented as a binary tree. Remember, a binary tree is where each parent had a maximum of two direct child nodes. What makes a heap special? Like a binary search tree, we add additional constraints. So the basics. Heaps are a collection of objects. As we add items to the heap, they are always added top to bottom, left to right. We completely fill in the level before moving onto the next. This means we don’t have to worry about the tree becoming imbalanced, like a binary search tree can. But it’s not just random things added in any random order. Depending on the type of heap, we care about the minimum or maximum value. What this means is do we want the top of the heap, our root node, to always contain the lowest value in the entire heap, or do we want the top of the heap to always contain the highest value? It all depends on what data we want to access most. For a min heap, any child must be greater than its parent node. For a max heap, any child must be less than its parent node. So let’s say we start off with an empty min heap. Then we add 10. This will be the rote node for now. Then we add 20. 20 is greater than 10, so it must be a child node. Since we filled the tree from left to right, it becomes a left child node. Then we add 15. 15 is greater than 10, so it becomes the right child node. Notice we don’t care if 15 is less than or greater than its sibling. That doesn’t matter at all. Since the root node now has two children, we must go a level deeper and begin to add nodes here. Let’s add 50. This will become the left child of 20. Now let’s add 18. The next available slot is the right child of the 20 node, so we’ll put it there and then do a check. Is 18 greater than 20? No, it’s not, so we swap the 18 and 20 nodes. Then we check is 18 is greater than its parent, 10, and it is, so now we’re done. This operation of swapping nodes is how the heap keeps itself organized. For one last item, let’s say we add five to the heap. 

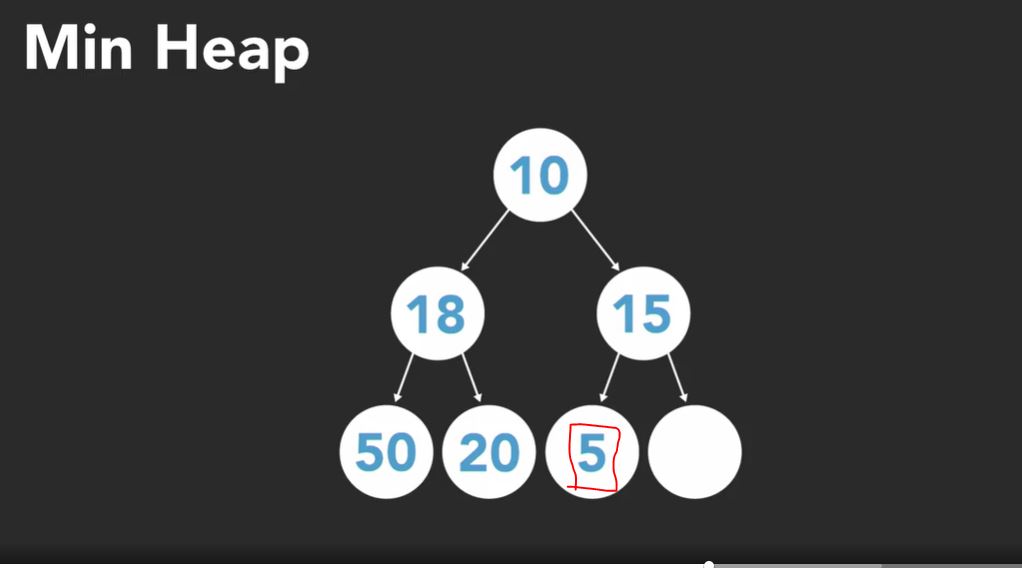
The next slot is the right child of 15, but we have to do some swapping. Five is less than 15, so we make five the new parent node. 

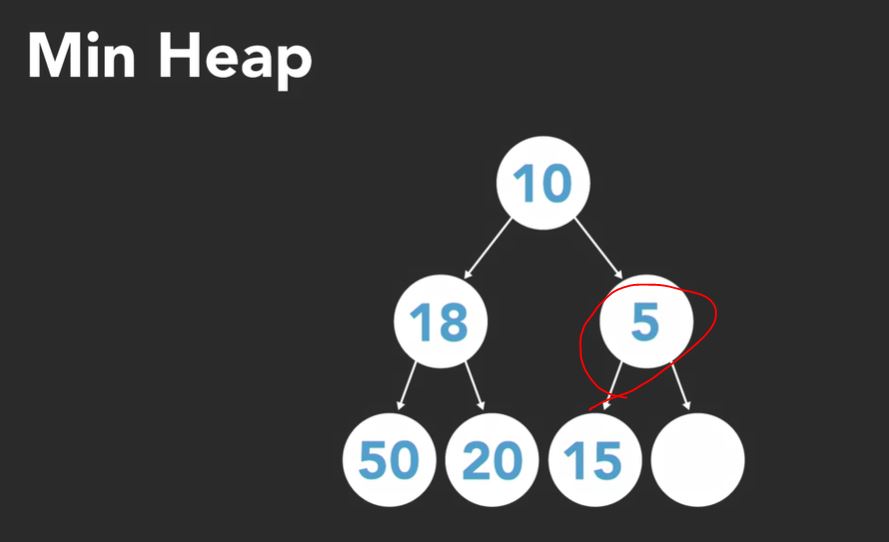
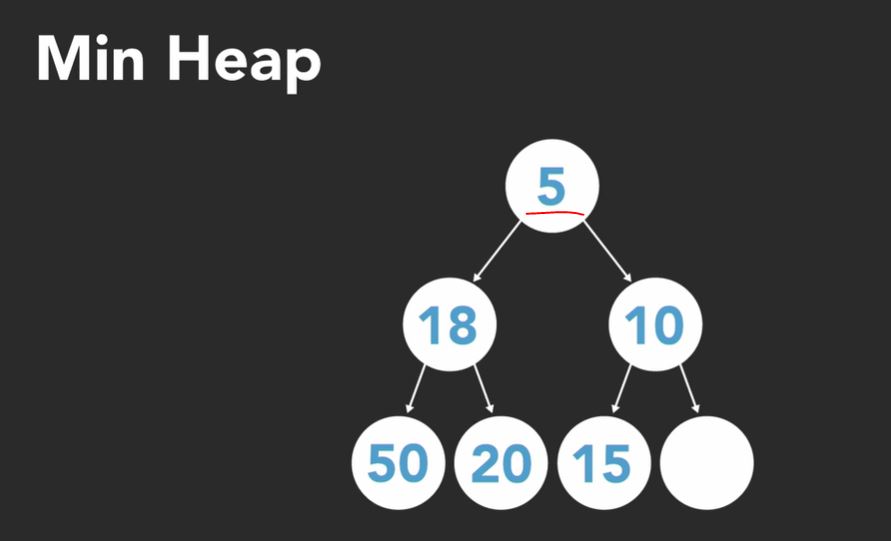
Then five is less than 10, so five becomes the new root node and we swap the nodes. In this way, the min heap always bubbles up the lowest value to the top of the heap. A max heap is exactly like this, but opposite.

Heaps don’t work for a lot of situations, but they are best for certain things, like priority queues and certain sorting algorithms.